Движок на дровах, или немного о теории BSP
Создание карт, как и любое другое искусство, требует от автора не только досконального владения его непосредственным инструментом, но также знания, хотя бы в общих чертах, фундаментальных основ той области, в которой он работает. Художники, например, для лучшего понимания строения человеческого тела изучают анатомию. Так же и в ремесле картостроителя — знание основных принципов 3D-графики для совершенствования профессионального мастерства дизайнера уровней просто необходимо.
В данной статье рассмотрен принцип работы 3D-движка на основе широко применяемой BSP-технологии. Продемонстрирован процесс формирования специального иерархического массива — древа BSP. Показано использование BSP-древа, а также пути его оптимизации.
Корень проблемы
Даже начинающий левел-дизайнер в курсе, что подавляющее большинство современных 3D-игр построено на основе так называемой полигонной графики. Это означает, что весь компьютерный мир и его объекты представлены в виде комбинации большого количества разных по форме и размерам плоских граней-многоугольников, называемых «полигонами». В таком мире (обычно именуемом «картой» или «уровнем»), например, цилиндр и конус будут выглядеть соответственно как призма и пирамида с правильным многоугольником в основании. При этом чем мельче разбиение на полигоны, тем выше детализация уровня и его реалистичность.
Вместе с тем, мало лишь спроектировать мир из полигонов. Необходимо сделать так, чтобы созданная трехмерная карта правильно отображалась на мониторе, причем в условиях постоянного изменения позиции наблюдателя в реальном времени. Таким образом, необходимо определить способ получения проекции объемной сцены на воображаемую поверхность экрана наблюдателя в зависимости его местоположения, ориентации взгляда и перспективы (рис. 1).
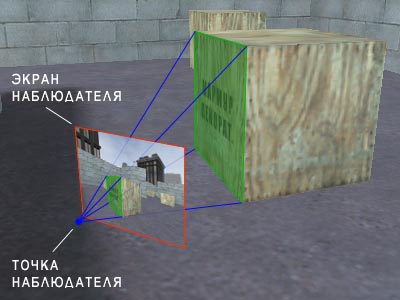
рис. 1
Проекция с учетом ориентации и перспективы — дело несложное, скажете вы. Но как же обойтись с теми частями карты, которые должны быть закрыты от взора наблюдателя, скажем, непрозрачной стеной или ящиком? Иными словами, необходимо определить такой способ проецирования 3D-мира на экран монитора, чтобы отображать только реально видимые из данной точки поверхности (или их видимые части).
На первый взгляд, достаточно ограничиться следующим алгоритмом:
Едва ли не единственное достоинство такого алгоритма состоит в том, что он предельно прост в реализации. Однако недостатки более весомы:
рис. 2
Вырастим дерево…
В связи с приведенными выше соображениями, был разработан алгоритм работы 3D-движка на основе так называемой технологии BSP, суть которой состоит в следующем.
Все полигоны нашего трехмерного уровня особым способом (об этом способе речь пойдет несколько позже) размещаются в специальном массиве, с помощью которого компьютер, зная местоположение точки наблюдателя (игрока), без дополнительной сортировки сможет в реальном времени определять последовательность прорисовки всех полигонов.
Что это за чудо-матрица, спросите вы. И как ее получить?
Задачи построения иерархии и осуществления сортировки в математике известны уже давно. В нашем же случае наиболее подходящей моделью искомого массива для полигонов является так называемое «древо». Такое «ботаническое» название обусловлено схематическим видом данного массива — он действительно напоминает дерево, правда перевернутое (рис. 3).
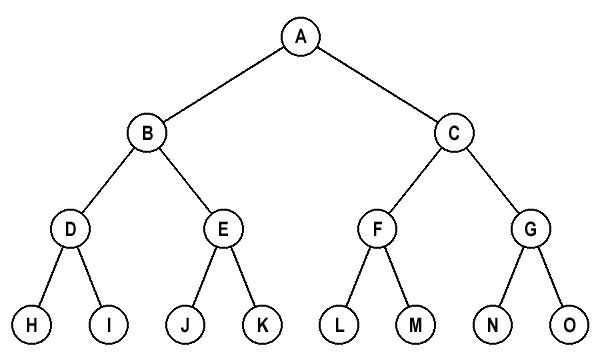
рис. 3
Как видно из рисунка, подобное «растение» состоит из узловых точек (называемых «нодами») и линий-связей между ними. У древа есть корень — некая самая главная узловая точка, связанная с одним или двумя нодами более низкого уровня. Те, в свою очередь, связаны с нодами еще более низкой иерархиии т.д. Ну, это все голая теория. Як кажуть у нас на Французщіні:), retournons aux nos moutons, т.е. вернемся к нашим баранам — в случае BSP-технологии в качестве нодов выступают полигоны карты, а само древо строится следующим образом — продемонстрируем на простом примере.
Пусть наша карта представляет собой комнату с прямоугольной колонной посредине (рис. 4).

рис. 4
Для простоты иллюстрации, отбросим пол и потолок — суть метода от этого не пострадает. Обозначим имеющиеся восемь стен-полигонов S1, S2… S8 (рис. 5).
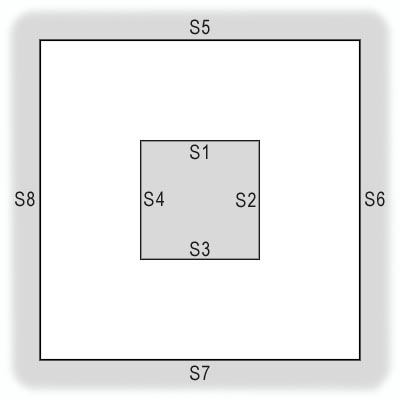
рис. 5
Пусть полигон S1 будет корнем нашего древа. Теперь продолжим плоскость полигона S1 таким образом, чтобы она прошла через всю карту. При этом, если какой-либо из полигонов разделится данной плоскостью надвое, получившиеся части будем считать отдельными поверхностями, соответственно их переименовав. В итоге получим следующую картину — см. рис. 6.
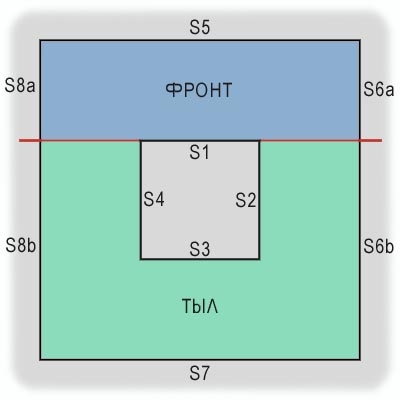
рис. 6
Как видно, плоскость разреза пересекла полигоны S6 и S8, и в результате вместо этих двух поверхностей мы получили четыре — S6a, S6b, S8a и S8b. Кроме того, относительно полигона S1 вся карта оказалась разбита на две самостоятельные части. Причем одна из них (фронтальная) находится полностью с лицевой части полигона S1, а вторая (тыльная) — полностью с оборотной стороны.
Теперь собственно о древе. Как мы уже определились, в качестве корня древа выступает полигон S1. Изобразим корневой нод S1 и пару исходящих из него связей с двумя нодами более низкого порядка (рис. 7). Слева от нода S1 будем размещать полигоны фронтальной части карты, а справа — тыльной, поэтому соответствующие линии-связи обозначим буквами «Ф» и «Т».
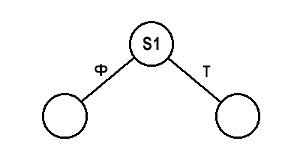
рис. 7
Рассматривая две полученные части карты по отдельности, выберем в каждой из них некий главный полигон, после чего в обеих частях осуществим описанную выше операцию разбиения. При этом заметим, что поскольку полигон S1 в древе уже учтен, он не входит ни в одну из двух рассматриваемых частей. Пусть во фронтальной части в качестве корня выбран полигон S5, а в тыльной — S2. В этом случае разбивка карты примет вид, показанный на рис. 8.
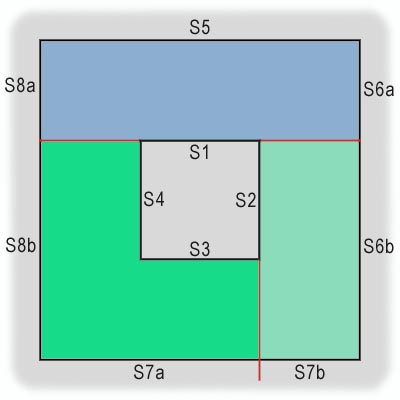
рис. 8
Как видно из рисунка, тыльная по отношению к S1 часть карты оказалась, в свою очередь, разбита надвое плоскостью полигона S2, причем полигон S7 также разделился на два полигона — S7a и S7b. Вместе с тем, фронтальная по отношению к S1 часть изменений не претерпела, т.к. она вся находится по одну сторону (собственно, лицевую) от секущей плоскости полигона S5.
Разместим выбранные два локальных корня S5 и S2 в нашем древе в качестве двух подчиненных ноду S1 (рис. 9).
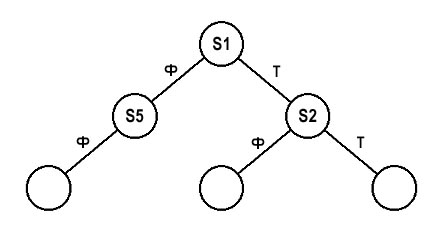
рис. 9
Так как полигон S2 разбил свое пространство на фронтальную и тыльную по отношению к самому себе части, то из нода S2, как и в случае с нодом S1, исходят две линии-связи — фронтальная и тыльная. По отношению к полигону S5, как уже было замечено, тыльной части не существует, поэтому из нода S5 будет исходить только фронтальная линия-связь.
Аналогичным образом продолжаем процесс разбиения пространства карты до тех пор, пока в древо не будут внесены все полигоны. В результате такой работы мы можем получить показанное на рис. 10 пространственное разбиение и соответствующее древо (рис. 11).
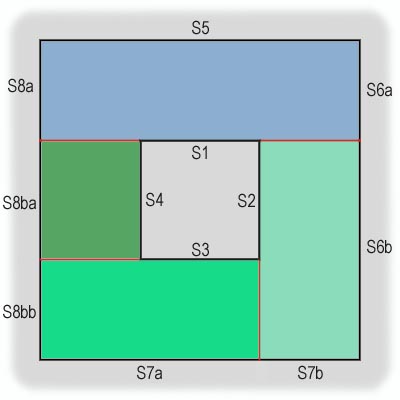
рис. 10
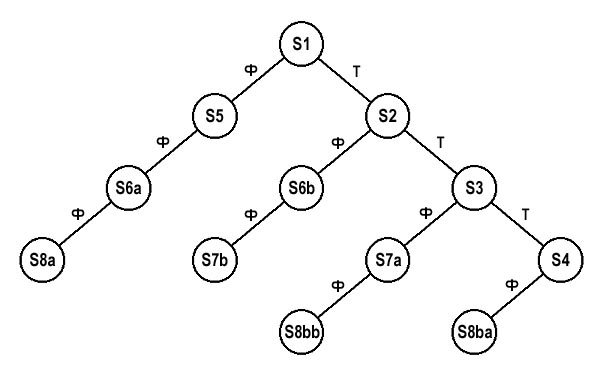
рис. 11
Изложенный выше процесс рекурсивного разбиения пространства карты на две части (т.е. двоичного разбиения) и определяет название технологии — Двоичное разбиение пространства, по-английски Binary Space Partitioning (сокращенно — BSP). Полученное же в результате древо именуется древом BSP (BSP Tree).
Деревянное рисование
Теперь о том, как с помощью «выращенного» BSP-древа определить порядок прорисовки полигонов карты в зависимости от местоположения наблюдателя. Для наглядности рассмотрим пару примеров.
Пусть точка наблюдателя V1 расположена так, как показано на рис. 12.
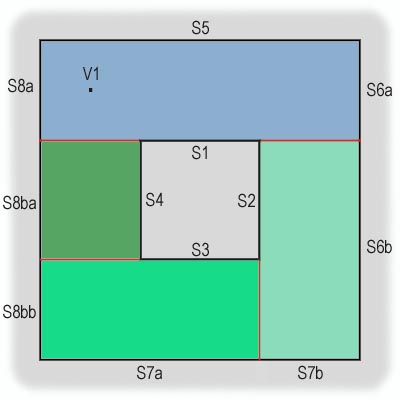
рис. 12
Начнем анализ с корневого нода древа. Так как точка наблюдателя находится с лицевой стороны полигона S1, то логично утверждать, что сначала следует прорисовать полигоны, находящиеся с тыльной стороны S1, затем сам полигон S1, ну, а потом уже иметь дело с полигонами, которые расположены спереди S1. Для лучшего запоминания такого порядка нанесем на древо в районе нода S1 соответствующую стрелку (рис. 13) — она будет определять порядок как бы «прохождения» нода S1.
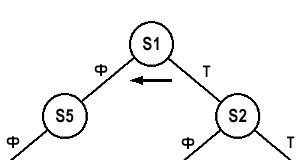
рис. 13
То же самое проделаем со всеми остальными нодами, из которых исходит хотя бы одна линия-связь вниз. При этом заметим, что в случае с нодами S2 и S3 направление прохождения будет обратным, так как полигоны S2 и S3 по отношению к точке наблюдателя обращены тыльной стороной. В результате стрелки расположатся так, как показано на рис. 14.
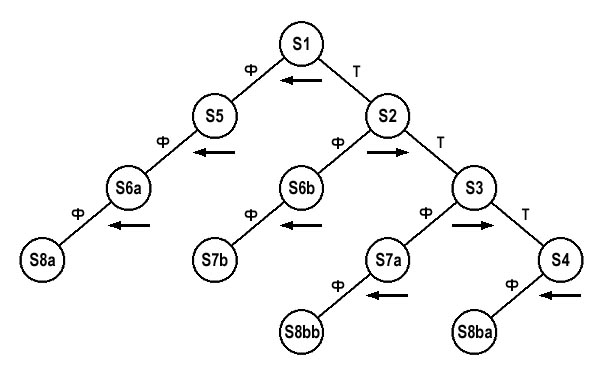
рис. 14
Теперь по полученной схеме определяем порядок прорисовки поверхностей карты. Начнем с корня древа нода S1. Для того, чтобы его пройти, как видно по стрелке, необходимо сначала пройти нод S2, затем прорисовать сам полигон S1, после чего пройти нод S5. Чтобы, в свою очередь, пройти по стрелке нод S2, нужно пройти нод S6b, затем прорисовать полигон S2, после чего пройти нод S3. Восстанавливая подобным образом логическую цепочку для всего древа, получим следующую последовательность прорисовки полигонов карты:
S6b — S7b — S2 — S7a — S8bb — S3 — S4 — S8ba — S1 — S5 — S6a — S8a
Заметим, что нас совершенно не интересуют полигоны, которые расположены тыльной стороной к точке наблюдения — все равно их не будет видно. Таким образом, удалив из указанной выше последовательности полигоны S2 и S3, получаем окончательный порядок прорисовки поверхностей:
S6b — S7b — S7a — S8bb — S4 — S8ba — S1 — S5 — S6a — S8a
Для полноты картины рассмотрим еще один вариант местоположения наблюдателя, — пусть он находится в точке V2 (рис. 15).
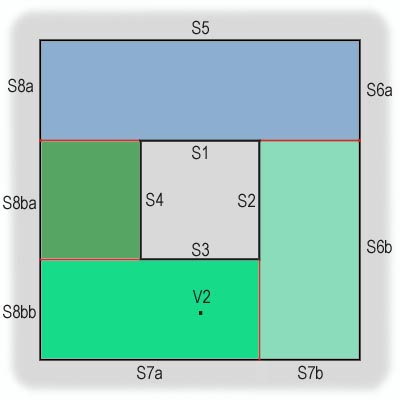
рис. 15
Произведя описанный выше анализ ориентации поверхностей по отношению к точке наблюдателя, получаем соответствующую схему прохождения нодов древа (рис. 16).
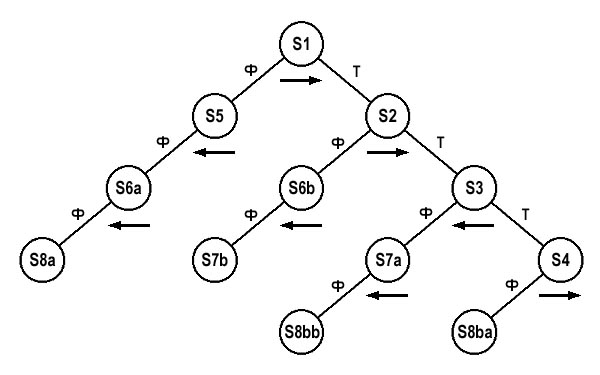
рис. 16
Действуя и далее по аналогии с предыдущим случаем, определяем искомый порядок прорисовки полигонов:
S5 — S6a — S8a — S6b — S7b — S8ba — S3 — S7a — S8bb
Оптимизация древа
Таким образом, BSP-древо позволяет движку корректно и быстро определять последовательность, с которой следует прорисовывать поверхности трехмерной карты.
Вместе с тем, сам по себе порядок внесения полигонов в BSP-древо является в общем случае произвольным. Поэтому для одной и той же карты можно построить множество вариантов BSP-древа, при этом мы получим не только разнообразие архитектуры (т.е. формы) древа, но также и разное количество нодов. Если, например, в нашем случае при построении древа полигоны вносить в последовательности S5; S6; S7; S8; S4; S3; S2; S1, то в результате ветвление линий-связей всегда будет идти в одну сторону (т.е. либо во фронтальном, либо в тыльном направлении), причем не произойдет ни одного дополнительного разбиения существующих поверхностей, количество нодов будет равно восьми (против двенадцати в предыдущем случае), а BSP-древо примет «линейный» вид (рис. 17).
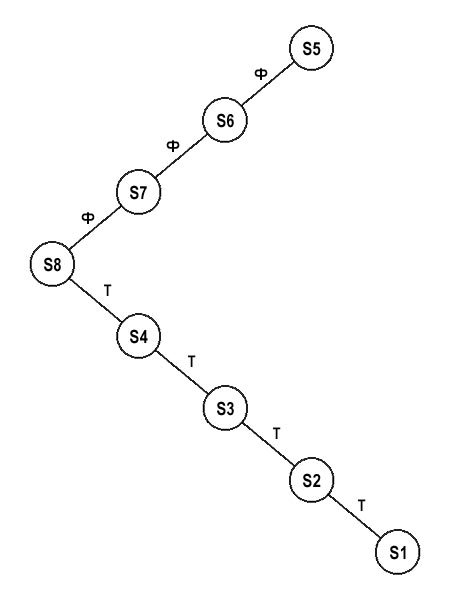
рис. 17
От того, какой именно вариант древа избран в качестве рабочего, зависит быстродействие движка.
С одной стороны, хорошо бы уменьшить количество дополнительных разбиений,т.е. минимизировать количество нодов. Ведь чем меньше нодов, тем быстрее происходит построение последовательности прорисовки, а также выведение полигонов на экран. С другой стороны, иногда соседние на карте полигоны желательно размещать по возможности ближе друг к другу и в структуре древа, в то время как общее количество нодов может не быть столь критичным. Кроме того, в некоторых случаях на первый план выходят другие требования, например минимизация глубины иерархической структуры (т.е. количество линий-связей между корнем и наиболее отдаленными от него нодами). Поэтому набор и значимость критериев оптимизации определяются конкретными особенностями движка и закладываются в алгоритм соответствующего BSP-компилятора.
Чем дальше в лес…
Подводя итог данной работы хотелось бы заметить, что применение BSP-технологии делает возможным реализацию ряда дополнительных способов оптимизации работы 3D-движка. Среди них метод на основе применения блоков визуальности (виз-блоков), позволяющий отсекать целые группы заведомо невидимых полигонов, а также использование так называемых HINT-брашей, с помощью которых можно влиять на процесс автоматизированного BSP-разбиения при компиляции.
BSP-древо весьма эффективно сочетается с так называемым глобальным усечением (global clipping). Дело в том, что наш взгляд (как в реальности, так и в компьютерном мире) не является панорамным, он ограничен неким объемным сектором обзора. Поэтому при обработке конечного изображения трехмерной сцены вполне можно отбросить выпадающие из поля нашего зрения участки карты. Соответствующий процесс фильтрации невидимых частей называется глобальным усечением и происходит он заметно быстрее с использованием древа BSP.
Как говорил Козьма Прутков, нельзя объять необъятное. Также и в рамках одной статьи невозможно рассказать обо всех нюансах BSP-ориентированного движка. В заключение лишь добавлю, что технологию двоичного разбиения пространства изобрели и впервые опубликовали в 1979–1980 годах три техасских ученых — Генри Фукс (Henry Fuchs), Зви Кедем (Zvi Kedem) и Брюс Нейлор (Bruce Naylor).
Чем они, несомненно, заслужили нашу признательность и уважение.
В данной статье рассмотрен принцип работы 3D-движка на основе широко применяемой BSP-технологии. Продемонстрирован процесс формирования специального иерархического массива — древа BSP. Показано использование BSP-древа, а также пути его оптимизации.
Корень проблемы
Даже начинающий левел-дизайнер в курсе, что подавляющее большинство современных 3D-игр построено на основе так называемой полигонной графики. Это означает, что весь компьютерный мир и его объекты представлены в виде комбинации большого количества разных по форме и размерам плоских граней-многоугольников, называемых «полигонами». В таком мире (обычно именуемом «картой» или «уровнем»), например, цилиндр и конус будут выглядеть соответственно как призма и пирамида с правильным многоугольником в основании. При этом чем мельче разбиение на полигоны, тем выше детализация уровня и его реалистичность.
Вместе с тем, мало лишь спроектировать мир из полигонов. Необходимо сделать так, чтобы созданная трехмерная карта правильно отображалась на мониторе, причем в условиях постоянного изменения позиции наблюдателя в реальном времени. Таким образом, необходимо определить способ получения проекции объемной сцены на воображаемую поверхность экрана наблюдателя в зависимости его местоположения, ориентации взгляда и перспективы (рис. 1).

рис. 1
Проекция с учетом ориентации и перспективы — дело несложное, скажете вы. Но как же обойтись с теми частями карты, которые должны быть закрыты от взора наблюдателя, скажем, непрозрачной стеной или ящиком? Иными словами, необходимо определить такой способ проецирования 3D-мира на экран монитора, чтобы отображать только реально видимые из данной точки поверхности (или их видимые части).
На первый взгляд, достаточно ограничиться следующим алгоритмом:
- Измеряем расстояние от точки наблюдателя до каждого полигона карты.
- Прорисовываем на экране проекции каждого из полигонов в порядке уменьшения их расстояния до точки наблюдателя.
Едва ли не единственное достоинство такого алгоритма состоит в том, что он предельно прост в реализации. Однако недостатки более весомы:
- Во-первых, при формировании очередного кадра изображения необходимо заново вычислять удаленность каждого из полигонов от точки наблюдения, производить необходимую сортировку и прорисовывать все имеющиеся на карте поверхности, что требует значительных ресурсов по быстродействию.
- Во-вторых, такой алгоритм не всегда будет работать корректно. В частности, в случае взаимного перекрытия нескольких полигонов (см. рис. 2) в принципе невозможно определить, какой из них следует прорисовывать в первую очередь, т.к. все они последовательно перекрывают друг друга — прямо как при игре в «пьяницу» — туз бьет короля, король — шестерку, а шестерка — туза!

рис. 2
Вырастим дерево…
В связи с приведенными выше соображениями, был разработан алгоритм работы 3D-движка на основе так называемой технологии BSP, суть которой состоит в следующем.
Все полигоны нашего трехмерного уровня особым способом (об этом способе речь пойдет несколько позже) размещаются в специальном массиве, с помощью которого компьютер, зная местоположение точки наблюдателя (игрока), без дополнительной сортировки сможет в реальном времени определять последовательность прорисовки всех полигонов.
Что это за чудо-матрица, спросите вы. И как ее получить?
Задачи построения иерархии и осуществления сортировки в математике известны уже давно. В нашем же случае наиболее подходящей моделью искомого массива для полигонов является так называемое «древо». Такое «ботаническое» название обусловлено схематическим видом данного массива — он действительно напоминает дерево, правда перевернутое (рис. 3).

рис. 3
Как видно из рисунка, подобное «растение» состоит из узловых точек (называемых «нодами») и линий-связей между ними. У древа есть корень — некая самая главная узловая точка, связанная с одним или двумя нодами более низкого уровня. Те, в свою очередь, связаны с нодами еще более низкой иерархии
Пусть наша карта представляет собой комнату с прямоугольной колонной посредине (рис. 4).

рис. 4
Для простоты иллюстрации, отбросим пол и потолок — суть метода от этого не пострадает. Обозначим имеющиеся восемь стен-полигонов S1, S2… S8 (рис. 5).

рис. 5
Пусть полигон S1 будет корнем нашего древа. Теперь продолжим плоскость полигона S1 таким образом, чтобы она прошла через всю карту. При этом, если какой-либо из полигонов разделится данной плоскостью надвое, получившиеся части будем считать отдельными поверхностями, соответственно их переименовав. В итоге получим следующую картину — см. рис. 6.

рис. 6
Как видно, плоскость разреза пересекла полигоны S6 и S8, и в результате вместо этих двух поверхностей мы получили четыре — S6a, S6b, S8a и S8b. Кроме того, относительно полигона S1 вся карта оказалась разбита на две самостоятельные части. Причем одна из них (фронтальная) находится полностью с лицевой части полигона S1, а вторая (тыльная) — полностью с оборотной стороны.
Теперь собственно о древе. Как мы уже определились, в качестве корня древа выступает полигон S1. Изобразим корневой нод S1 и пару исходящих из него связей с двумя нодами более низкого порядка (рис. 7). Слева от нода S1 будем размещать полигоны фронтальной части карты, а справа — тыльной, поэтому соответствующие линии-связи обозначим буквами «Ф» и «Т».

рис. 7
Рассматривая две полученные части карты по отдельности, выберем в каждой из них некий главный полигон, после чего в обеих частях осуществим описанную выше операцию разбиения. При этом заметим, что поскольку полигон S1 в древе уже учтен, он не входит ни в одну из двух рассматриваемых частей. Пусть во фронтальной части в качестве корня выбран полигон S5, а в тыльной — S2. В этом случае разбивка карты примет вид, показанный на рис. 8.

рис. 8
Как видно из рисунка, тыльная по отношению к S1 часть карты оказалась, в свою очередь, разбита надвое плоскостью полигона S2, причем полигон S7 также разделился на два полигона — S7a и S7b. Вместе с тем, фронтальная по отношению к S1 часть изменений не претерпела, т.к. она вся находится по одну сторону (собственно, лицевую) от секущей плоскости полигона S5.
Разместим выбранные два локальных корня S5 и S2 в нашем древе в качестве двух подчиненных ноду S1 (рис. 9).

рис. 9
Так как полигон S2 разбил свое пространство на фронтальную и тыльную по отношению к самому себе части, то из нода S2, как и в случае с нодом S1, исходят две линии-связи — фронтальная и тыльная. По отношению к полигону S5, как уже было замечено, тыльной части не существует, поэтому из нода S5 будет исходить только фронтальная линия-связь.
Аналогичным образом продолжаем процесс разбиения пространства карты до тех пор, пока в древо не будут внесены все полигоны. В результате такой работы мы можем получить показанное на рис. 10 пространственное разбиение и соответствующее древо (рис. 11).

рис. 10

рис. 11
Изложенный выше процесс рекурсивного разбиения пространства карты на две части (т.е. двоичного разбиения) и определяет название технологии — Двоичное разбиение пространства, по-английски Binary Space Partitioning (сокращенно — BSP). Полученное же в результате древо именуется древом BSP (BSP Tree).
Деревянное рисование
Теперь о том, как с помощью «выращенного» BSP-древа определить порядок прорисовки полигонов карты в зависимости от местоположения наблюдателя. Для наглядности рассмотрим пару примеров.
Пусть точка наблюдателя V1 расположена так, как показано на рис. 12.

рис. 12
Начнем анализ с корневого нода древа. Так как точка наблюдателя находится с лицевой стороны полигона S1, то логично утверждать, что сначала следует прорисовать полигоны, находящиеся с тыльной стороны S1, затем сам полигон S1, ну, а потом уже иметь дело с полигонами, которые расположены спереди S1. Для лучшего запоминания такого порядка нанесем на древо в районе нода S1 соответствующую стрелку (рис. 13) — она будет определять порядок как бы «прохождения» нода S1.

рис. 13
То же самое проделаем со всеми остальными нодами, из которых исходит хотя бы одна линия-связь вниз. При этом заметим, что в случае с нодами S2 и S3 направление прохождения будет обратным, так как полигоны S2 и S3 по отношению к точке наблюдателя обращены тыльной стороной. В результате стрелки расположатся так, как показано на рис. 14.

рис. 14
Теперь по полученной схеме определяем порядок прорисовки поверхностей карты. Начнем с корня древа нода S1. Для того, чтобы его пройти, как видно по стрелке, необходимо сначала пройти нод S2, затем прорисовать сам полигон S1, после чего пройти нод S5. Чтобы, в свою очередь, пройти по стрелке нод S2, нужно пройти нод S6b, затем прорисовать полигон S2, после чего пройти нод S3. Восстанавливая подобным образом логическую цепочку для всего древа, получим следующую последовательность прорисовки полигонов карты:
S6b — S7b — S2 — S7a — S8bb — S3 — S4 — S8ba — S1 — S5 — S6a — S8a
Заметим, что нас совершенно не интересуют полигоны, которые расположены тыльной стороной к точке наблюдения — все равно их не будет видно. Таким образом, удалив из указанной выше последовательности полигоны S2 и S3, получаем окончательный порядок прорисовки поверхностей:
S6b — S7b — S7a — S8bb — S4 — S8ba — S1 — S5 — S6a — S8a
Для полноты картины рассмотрим еще один вариант местоположения наблюдателя, — пусть он находится в точке V2 (рис. 15).

рис. 15
Произведя описанный выше анализ ориентации поверхностей по отношению к точке наблюдателя, получаем соответствующую схему прохождения нодов древа (рис. 16).

рис. 16
Действуя и далее по аналогии с предыдущим случаем, определяем искомый порядок прорисовки полигонов:
S5 — S6a — S8a — S6b — S7b — S8ba — S3 — S7a — S8bb
Оптимизация древа
Таким образом, BSP-древо позволяет движку корректно и быстро определять последовательность, с которой следует прорисовывать поверхности трехмерной карты.
Вместе с тем, сам по себе порядок внесения полигонов в BSP-древо является в общем случае произвольным. Поэтому для одной и той же карты можно построить множество вариантов BSP-древа, при этом мы получим не только разнообразие архитектуры (т.е. формы) древа, но также и разное количество нодов. Если, например, в нашем случае при построении древа полигоны вносить в последовательности S5; S6; S7; S8; S4; S3; S2; S1, то в результате ветвление линий-связей всегда будет идти в одну сторону (т.е. либо во фронтальном, либо в тыльном направлении), причем не произойдет ни одного дополнительного разбиения существующих поверхностей, количество нодов будет равно восьми (против двенадцати в предыдущем случае), а BSP-древо примет «линейный» вид (рис. 17).

рис. 17
От того, какой именно вариант древа избран в качестве рабочего, зависит быстродействие движка.
С одной стороны, хорошо бы уменьшить количество дополнительных разбиений,
Чем дальше в лес…
Подводя итог данной работы хотелось бы заметить, что применение BSP-технологии делает возможным реализацию ряда дополнительных способов оптимизации работы 3D-движка. Среди них метод на основе применения блоков визуальности (виз-блоков), позволяющий отсекать целые группы заведомо невидимых полигонов, а также использование так называемых HINT-брашей, с помощью которых можно влиять на процесс автоматизированного BSP-разбиения при компиляции.
BSP-древо весьма эффективно сочетается с так называемым глобальным усечением (global clipping). Дело в том, что наш взгляд (как в реальности, так и в компьютерном мире) не является панорамным, он ограничен неким объемным сектором обзора. Поэтому при обработке конечного изображения трехмерной сцены вполне можно отбросить выпадающие из поля нашего зрения участки карты. Соответствующий процесс фильтрации невидимых частей называется глобальным усечением и происходит он заметно быстрее с использованием древа BSP.
Как говорил Козьма Прутков, нельзя объять необъятное. Также и в рамках одной статьи невозможно рассказать обо всех нюансах BSP-ориентированного движка. В заключение лишь добавлю, что технологию двоичного разбиения пространства изобрели и впервые опубликовали в 1979–1980 годах три техасских ученых — Генри Фукс (Henry Fuchs), Зви Кедем (Zvi Kedem) и Брюс Нейлор (Bruce Naylor).
Чем они, несомненно, заслужили нашу признательность и уважение.